Bfs for Binary Tree Keep Track of Levels

Coding Interview Tree Traversal Crash Course – The Only One You'll Ever Need

Are you preparing for coding interviews? I designed a crash course series to help you out.

I'm Lynn, a software engineer and a recent graduate from the University of Chicago. This is the second course in my Coding Interview Crash Course Series. Feel free to check out my YouTube channel, Lynn's DevLab, to stay updated on this series.

This crash course is about Tree Traversal. If you just want to dive right in, you can find the course here (and linked at the bottom of this article). If you want a little more info, read on. 😎

Who is the Course for and What are Tree Traversal Algorithms? 🌳

You will get the most of this course if you already know a bit about the Tree data structure. Check out these tutorials if you need a refresher.

We will cover the traversal algorithms for both Binary Trees and N-ary Trees (in which each parent node has an arbitrary number of children).

If you have heard about Binary Search Trees (BST) before, that's a special type of Binary Tree so the techniques we are going to learn here also apply.

Trees are a favorite interview subject among top tech companies like Google, Microsoft, and Facebook, so let's crunch this topic!

We will learn about four traversal techniques and solve their corresponding LeetCode problems hands-on.

The four techniques are:

Pre-order (Depth-First Search, DFS)
Post-order
In-order
Level-order (Breadth-First Search, BFS).

Course Outline

This course video runs for a total of 30 minutes and features:

A high-level description of the four traversal techniques: pre-order, post-order, in-order, and level-order
Recursive implementations of pre-order, post-order, and in-order (Note: this doesn't apply to level-order)
Iterative implementations of pre-order, post-order, in-order, and level-order
An extension of the templates from Binary Trees to N-ary Trees

Let's dive into each of the four techniques below.

Tree Traversal Demonstration Using an Example Tree

We will use the following tree to demonstrate the output from the four traversal techniques.

Note that this tree is a simple Binary Tree, not a Binary Search Tree (BST). A BST is a special type of Binary Tree, so our techniques also apply. Also, in-order traversal becomes especially interesting when we work with a BST, as we will see below.

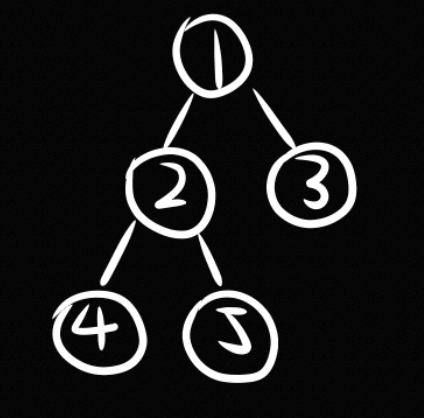
An example Binary Tree. Note that it's not a Binary Search Tree (BST).

Given this tree, the traversal result from the four techniques are as follows:

Pre-order: 1, 2, 4, 5, 3
Post-order: 4, 5, 2, 3, 1
In-order: 4, 2, 5, 1, 3
Level-order: 1, 2, 3, 4, 5

Pre-order Traversal

Pre-order traversal is also known as Depth-First Search (DFS) if we analyze the tree as a graph and take the tree root node as our starting node in the search.

As in the example above, we go all the way down to the leftmost node before visiting any other node that is a left child of some parent node.

Pre-order traversal allows us to explore roots before leaves, and is hence ideal for tasks like copying a tree.

Post-order Traversal

Post-order traversal does the opposite of pre-order traversal, allowing us to explore leaves before roots.

In-order Traversal

In-order traversal is especially useful for flattening a tree into an array representation.

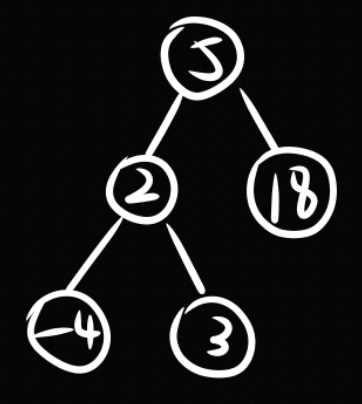
For a Binary Search Tree like below, in-order traversal outputs an array in a sorted, non-decreasing order: -4, 3, 2, 5, 18.

Level-order Traversal

Level-order traversal is also known as Breadth-First Search (BFS) if we consider the tree as a graph and start our search from the tree root node.

We visit every node on the current level (depth) before moving onto those on the next level. Effectively, we visit the immediate neighbor of (one step away from) our current node before visiting neighbors that are farther away.

How to Implement these Four Techniques

We will use the following definition for a node of a Binary Tree:

                # Definition for a binary tree node. # class TreeNode: #     def __init__(self, val=0, left=None, right=None): #         self.val = val #         self.left = left #         self.right = right

Recursive implementation

Recursive implementations are the most straightforward. The most important thing to remember is the order in which we concatenate the results from the two recursive calls (one on the left subtree and one on the right subtree) with the value of the current node.

                def preorder(root):     if not root:         return []     return [root.val] + preorder(root.left) + preorder(root.right)

                def postorder(root):     if not root:         return []     return postorder(root.left) + postorder(root.right) + [root.val]

                def inorder(root):     if not root:         return []     return inorder(root.left) + [root.val] + inorder(root.right)

Iterative implementation

Compared to recursive implementations, iterative implementations are non-trivial. Most require that we use either a stack or a queue to keep track of the nodes that we need to visit.

                def preorder(self, root):     if not root:         return []     ret = []     stack = [root]     while stack:         node = stack.pop()         ret.append(node.val)         # note that we append the right child before the left child         if node.right:             stack.append(node.right)         if node.left:             stack.append(node.left)     return ret

                def postorder(self, root):     if not root:         return []     from collections import deque     ret = deque()     stack = [root]     while stack:         node = stack.pop()         ret.appendleft(node.val)         if node.left:             stack.append(node.left)         if node.right:             stack.append(node.right)     return ret

The implementation for in-order traversal looks quite different from pre-order and post-order:

                def inorder(self, root):     if not root:         return []     ret = []     stack = []     while root is not None or stack:         while root is not None:             stack.append(root)             root = root.left         root = stack.pop()         ret.append(root.val)         root = root.right     return ret

Lastly, we have level-order traversal, where we will output the result as [[nodes on the first level], [nodes on the second level], [nodes on the third level], ...].

                def levelorder(self, root):     if not root:         return []     ret = []     from collections import deque     queue = deque([root])     while queue:         ret_row = []         # fixed size for current level         for _ in range(len(queue)):             node = queue.popleft()             ret_row.append(node.val)             if node.left:                 queue.append(node.left)             if node.right:                 queue.append(node.right)         ret.append(ret_row)     return ret

N-ary Trees

We now extend our templates from handling Binary Trees to handling N-ary Trees. We use the following definition for the node of an N-ary Tree:

                class Node:     def __init__(self, val=None, children=[]):         self.val = val         self.children = children

To extend our iterative implementations to handle N-ary Trees, all we need to do is to make sure that we are appending the child nodes that we will visit in a correct order.

Recall that in pre-order traversal, we appended the right child before the left child. So when appending the children of a node of an N-ary Tree, we need to reverse the list of children.

                def preorder(self, root):     if not root:         return []     ret = []     stack = [root]     while stack:         node = stack.pop()         ret.append(node.val)         # reverse the list of children         for child in node.children[::-1]:             stack.append(child)     return ret

For the other traversal techniques, since we are appending the children from the left to the right, we can iterative over the list of children normally:

                def postorder(self, root):     if not root:         return []     from collections import deque     ret = deque()     stack = [root]     while stack:         node = stack.pop()         ret.appendleft(node.val)         for child in node.children:             stack.append(child)     return ret

                def levelorder(self, root):     if not root:         return []     ret = []     from collections import deque     queue = deque([root])     while queue:         ret_row = []         # fixed size for current level         for _ in range(len(queue)):             node = queue.popleft()             ret_row.append(node.val)             for child in node.children:                 queue.append(child)         ret.append(ret_row)     return ret

And now we can apply our tree traversal templates to trees that have an arbitrary number of children at each node.

Conclusion

In this crash course on tree traversal, we learned four techniques: pre-order, post-order, in-order, and level-order. We discussed how they differ and what tasks they are best for.

We also implemented them both in a recursive fashion and in an iterative one. Last but not least, we extended the techniques to deal with not only Binary Trees, but N-ary Trees.

I hope now you feel more confident about tree traversal interview questions. This is also a nice segue into the topic of my next crash course on graph traversal.

With the knowledge of pre-order traversal and level-order traversal, DFS and BFS won't be completely out of the blue for you 🤓 I will even talk about how I applied graph traversal when developing an algorithm for my match-three game, Clicky Galaxy, so stay tuned!